-
基本資訊
- 作者: 許志明
-
- 強度門檻化的優勢
- 直觀性
- 實現的單純性
- 計算速度快
- 常見的門檻化類別
- 門檻為一常數: 整體門檻化 (globalthresholding)
- 門檻值會變動: 局部門檻化 (localthresholding)
- 門檻值和空間座標有關: 動態門檻化 (dynamicthresholding)
- 基本原理
- 影像為陰暗背景和明亮物體組成
- 選定一個分開兩物體的門檻值
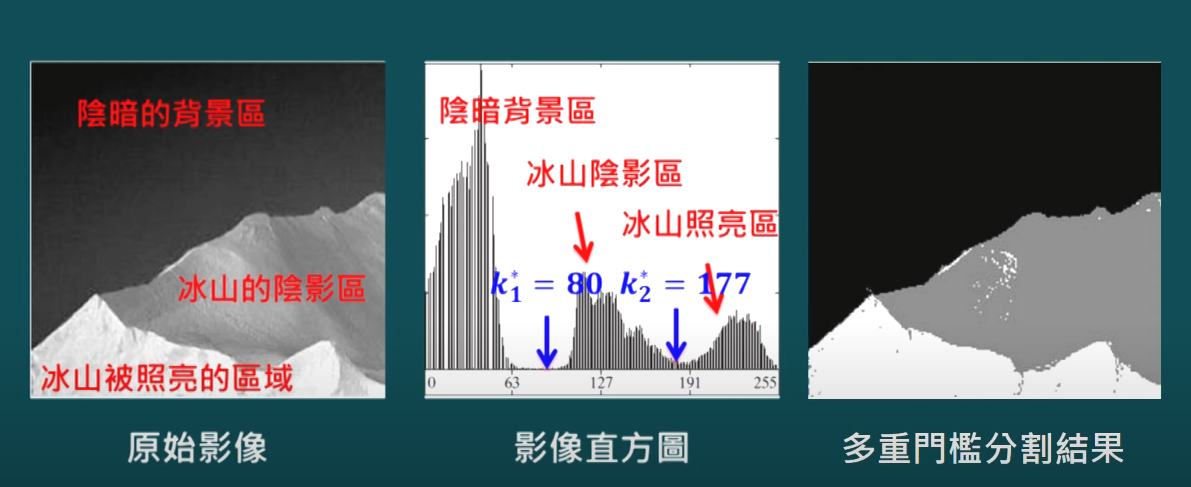
- 較複雜情形時,如影像為陰暗背景和兩個明亮物體組成,選定兩個分開三物體 的門檻值
- 門檻化影響因素
- 尖峰之間的分隔度
- 物體和背景相對大小
- 影像反射性質的均勻性
- 影像中的雜訊
- 照明光源的均勻性
- 強度門檻化的優勢
-
- 自動估測門檻值的演算法
- 選取門檻T的初始估測值 產生兩組像素G_1和G_2
- 計算出GI和G2區域的平均強度m_1和m_2
- 計算新的門檻值T’=0.5(m_1+m_2)
- 重複以上三個步驟直到T值差異小於預設的△T
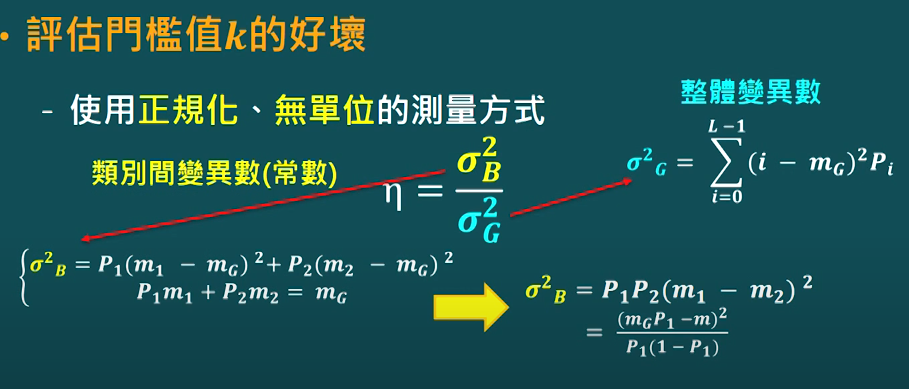
- Otsu自動門檻化方式
- 重要性質
- 使類別間的變異數最大化
- 好的門檻化下各類別,它們的像素強度值應該很不同
- 完全依據影像直方圖執行運算







- 重要性質
- 例子
- 自動估測門檻值的演算法
-
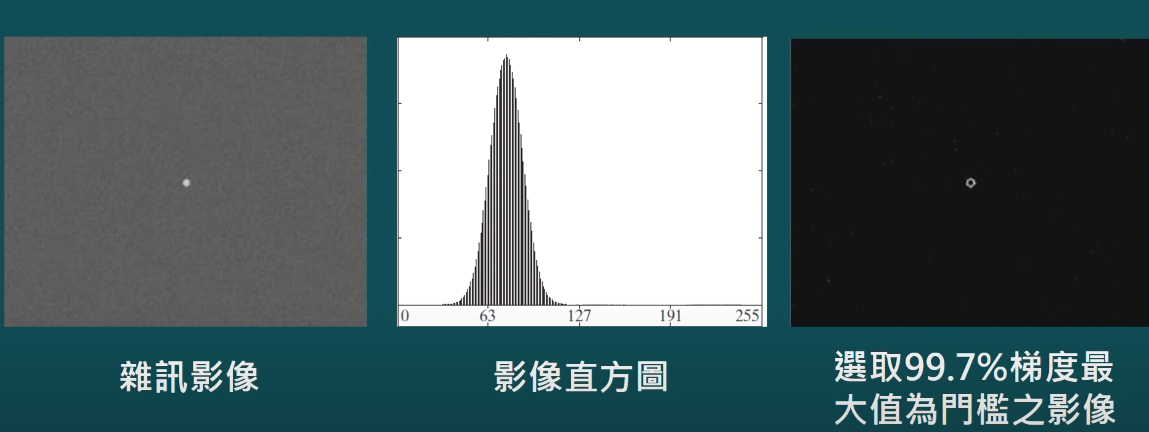
- 雜訊會使門檻值失效
- 當雜訊無法降低
- 門檻化為分割方法
- 增強效能方法:門檻化之前先將影像平滑處理
- 物體區域小到對直方圖的貢獻相較於雜訊而言小的多時,單純使用平滑+otsu會無效
- 直方圖門檻化的特性
- 直方圖的尖峰是高、窄、對稱
- 直方圖有深的山谷特徵
- 直方圖不受物體和背景的相對大小所影響
- 只考慮靠近物體與背景間邊緣的那些像素強度分布
- 只考慮靠近物體與背景間邊緣的那些像素分布
- 假設物體與背景間的邊緣是已知的情況下
- 可以改善直方圖模式的對稱性直方圖
- 實際上,這個邊緣資訊在分割的過程中是不可得的
- 可由計算像素的梯度或拉普拉斯準則找出邊緣

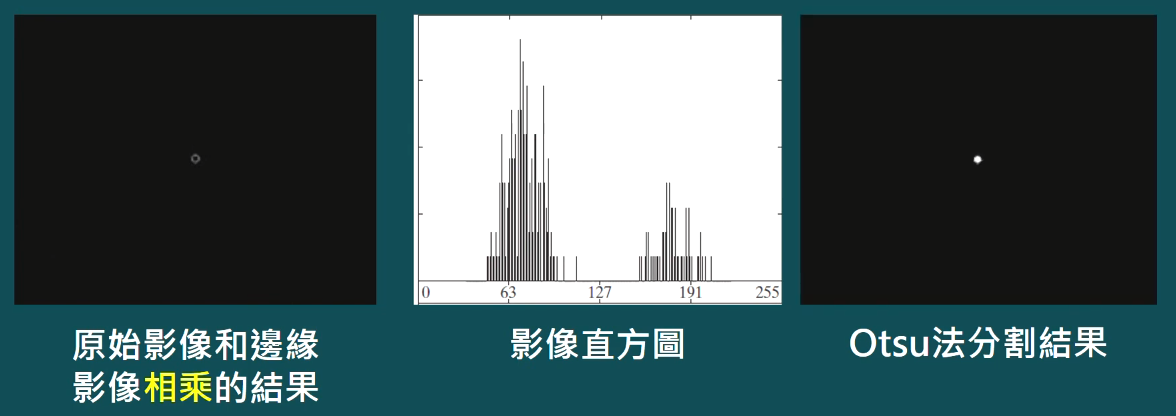
- 演算法
- 計算影像f(x, y)梯度或拉普拉斯絕對值
- 指定門檻值形成二值影像g_T(x, y)
- 以f(x, y)中和g_T(x, y)非零像素同位置像素計算直方圖
- 以Otsu法計算門檻值
- 例子
- 雜訊會使門檻值失效
-


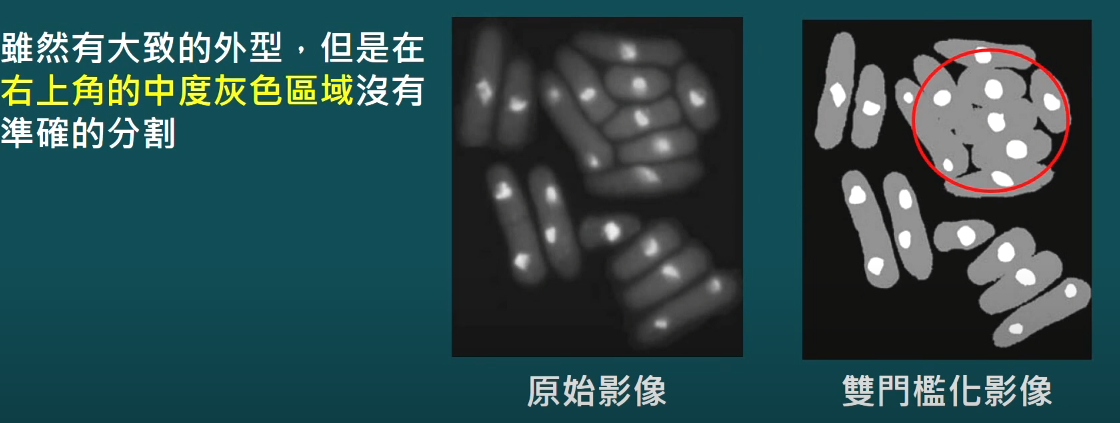
- 演算法
- 例子
- 多變數門檻化基本概念
- 一個以上的變數描述影像
- 每個像素以紅、藍、綠三個成分形成彩色影像
- 可表示為一個三維向量z=(Z1,Z2,Z3)
- 三維點常稱為體素(voxel)
- 可視為一個距離的計算
- 擷取一個特定的色彩範圍區域(例如黃色)
- 三維向量距離空間的討論
- 歐基里德距離
- 馬氏(MahaIanobis)距離
- 邊界盒(boundingbox)距離
-
- 影響門檻化演算法的效能
- 影像雜訊和非均勻照明的因數
- 影像平滑和用邊緣資訊,可幫助分割效能
- 遇到影像局部照明或反射不均勻時則仍影響著影像分割的成敗
- 可變門檻的三種方法
- 影像分區進行門檻化
- 將一張影像切成不重疊的矩形
- 用於補償照明、反射的非均勻性
- 矩形夠小使得區域內照明約略均勻

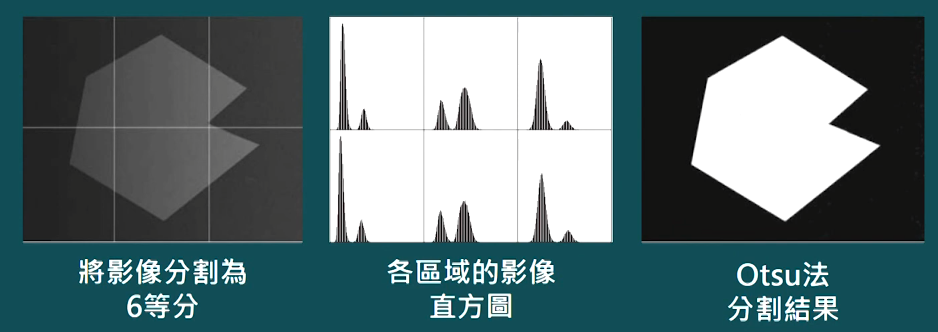
- 物體有明顯分區時才好使用,如果擷取區域僅有一物體則會失敗
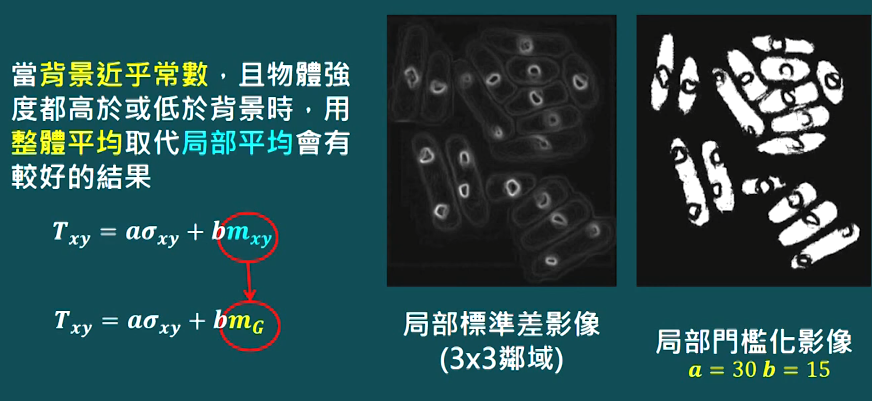
- 基於局部影像性質的可變門檻化
- 用移動平均進行門檻化
- 影像分區進行門檻化
- 影響門檻化演算法的效能
-
- 以區域為基礎的分割類型
- 區域成長
- 像素或子區域根據預先的定義聚合成長
- 從一個種子出發
- 性質相似的點進行聚合
- 預先定義的性質
- 強度、色度、紋理等
- 選擇相似性準則
- 想解決的問題類型
- 影像資料類型
- 區域成長終止原則:無像素能滿足被包括進該區域的準則時
- 演算法
- f(x, y)為輸入影像
- S(x,y)代表含有非零像素的種子點陣列
- Q為每個(x,y)位置要運用的述詞(判斷相似的準則)
- 找出s(x,所有連通成分並侵蝕,直到每一連通成分為單一像素點
- 形成影像f_Q(x, y)
- 1 if Q is true
- 0 if Q is not true
- 令g為輸出影像,對S(x, y)中每一個種子點和以八連通相接的點,加入g影像中
- 將g輸出影像中的每個連通成分以不同的區域標記標示,最後得到區域成長法的分割影像

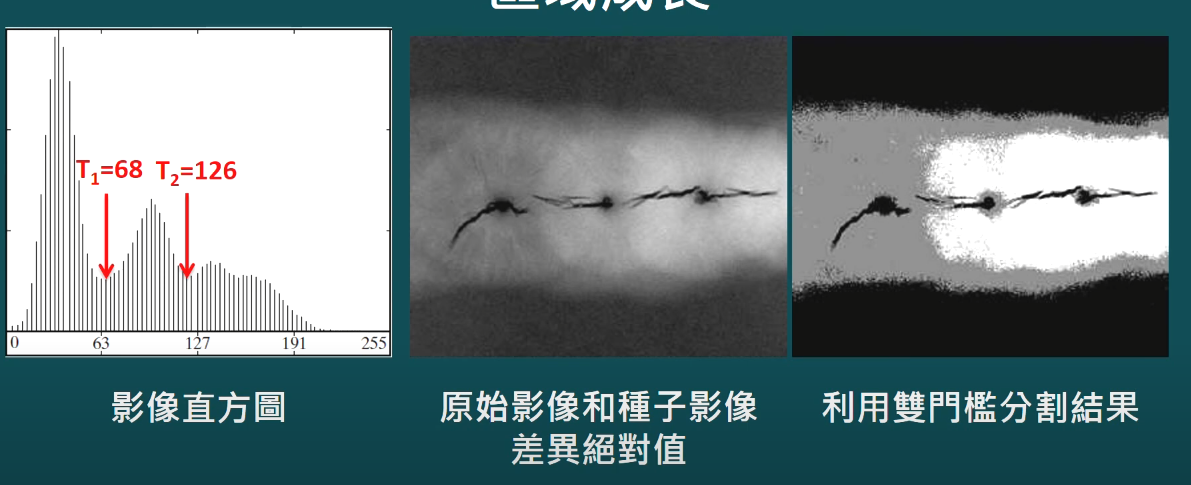
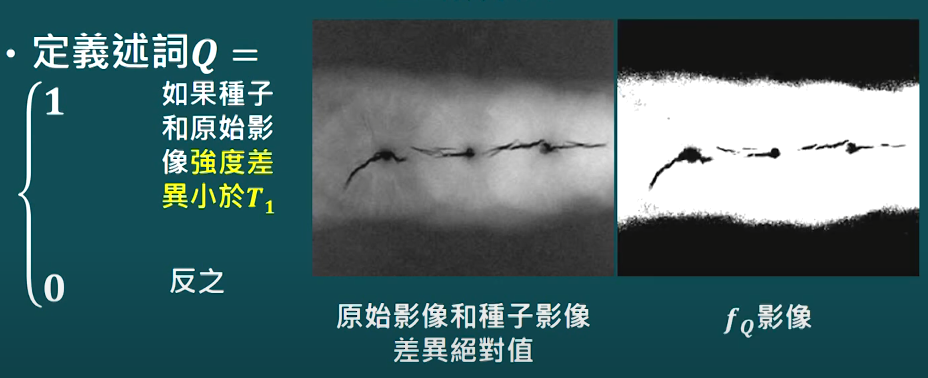

- 像素或子區域根據預先的定義聚合成長
- 區域分裂與合併
- 區域分裂
- 區域合併
- 使用區域分裂,最終的分割可能會有一些相同性質與相同區域的缺點,因次再使用區域合併來補救

- 演算法
- 例子
- 圖為566x566的X光影像
- 欲分割出環形的稀疏物質
- 稀疏物質特性
- 有較大標準差
- 平均強度大於背景,小於高密度區


- 區域分裂
- 區域成長
- 以區域為基礎的分割類型
-


- 基本概念
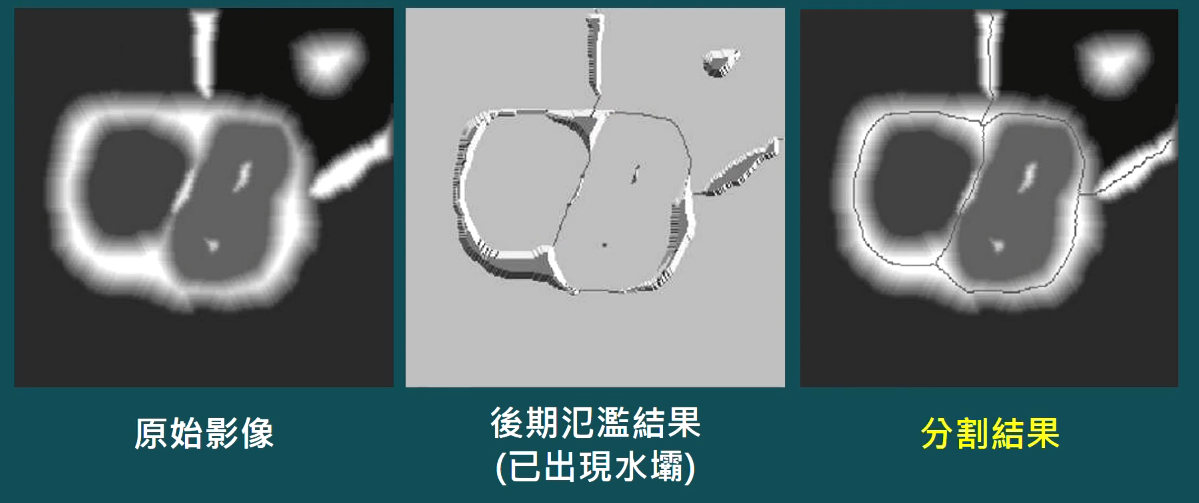
- 想像在區域最小值處鑽孔讓水注入
- 水位以均勻速度上升
- 到快要匯流時建立水壩阻隔
- 其水壩處就是分水線,也就是影像的連續邊界
- 例子
- 水壩的建造
- 以二值影像為基礎
- 以形態學的膨脹來建立
- 設M1、M2為區域極小點的集合
- C_n一1(M1)為第n-1階段從M1氾濫的水集合
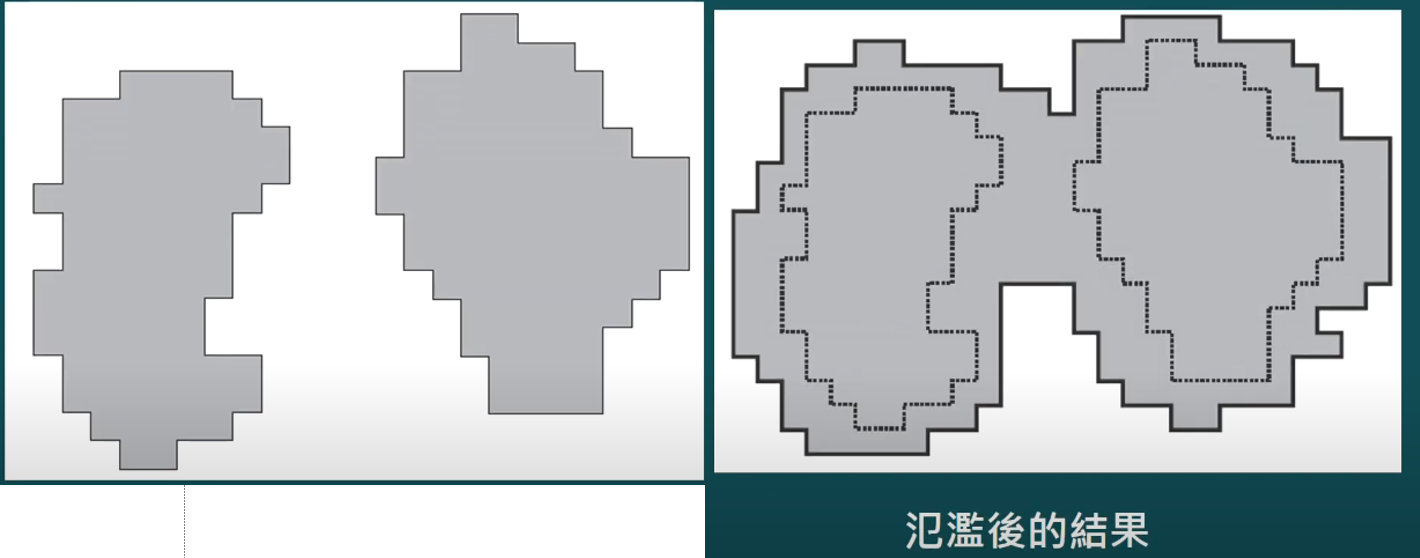
- 兩個集水區形成兩個連通成分
- 令連通成分為q
- 膨脹成分必被限制在q
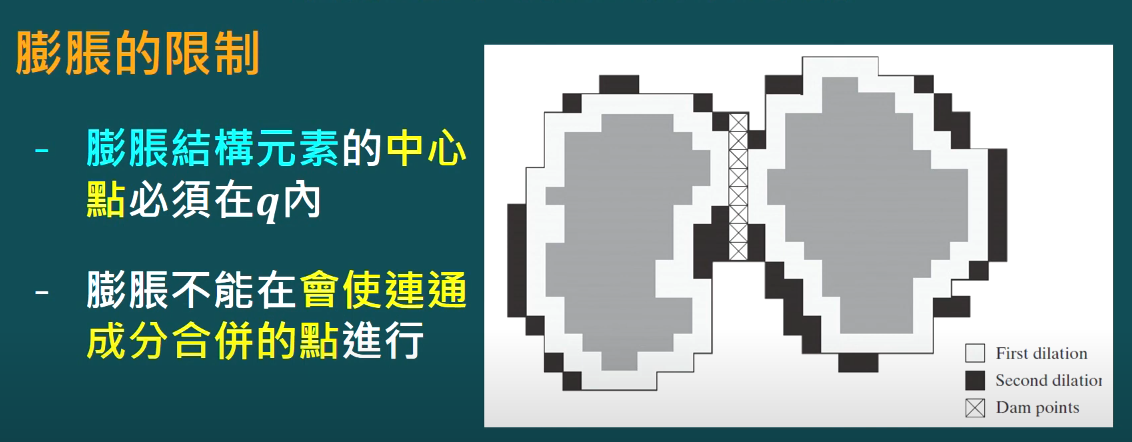
-